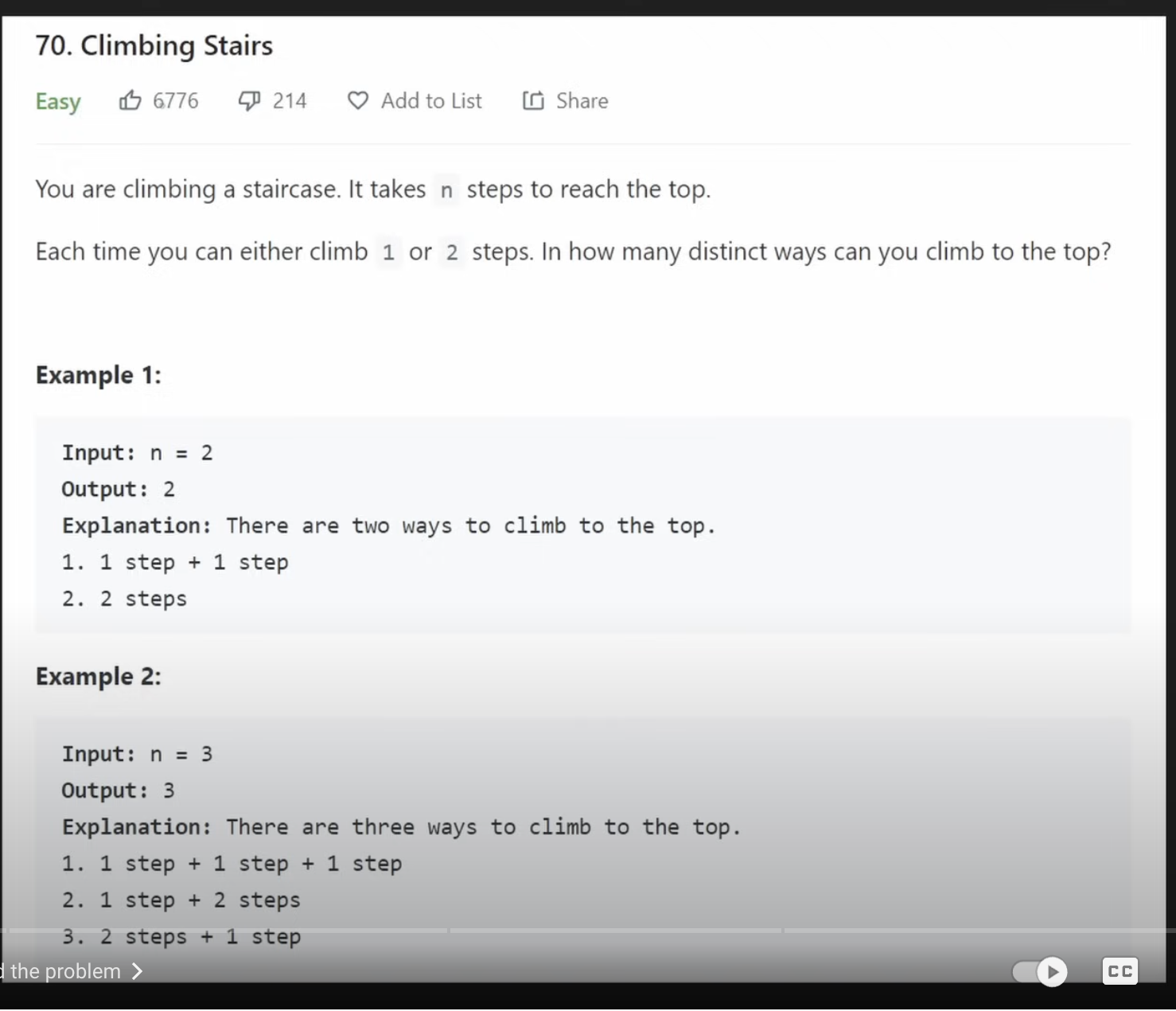
This is a dynamic programming problem
Stairs.
Start at the top of the stairs, say step 5 From step 5, how many different ways can you get to 5? 1 way. Just stay there
From Step 4, how many different ways can you get to 5? 1 way. 1 step From Step 3, how many different ways can you get to 5? you can take one step (and follow the 4 stream), or you can take two steps (and follow the 5 stream). Thus there are 1 + 1 ways. From step 2, you repeat. there are 2 + 1 ways Then step 1 gives you 3 + 2 ways Step 0 gives you 5 + 3 ways
A dynamic programming problem is one that can be broken down into simpler overlapping subproblems that can be solved independently and then combined to solve the larger problem. It typically exhibits two key properties:
-
Optimal Substructure: The solution to the larger problem can be constructed from the solutions of its subproblems. That is, an optimal solution to the problem contains within it optimal solutions to subproblems.
-
Overlapping Subproblems: The problem can be divided into subproblems that are reused multiple times. Instead of solving the same subproblems repeatedly, dynamic programming saves the results of these subproblems in a table (usually called memoization or tabulation), ensuring that each subproblem is solved only once.
Common examples include the Fibonacci sequence, shortest path problems (like the Bellman-Ford algorithm), and the Knapsack problem.